Databricks Community

YoyoHappy · ‎05-23-2025

Introduction

IRR is a common method used by financial personnel to evaluate the financial benefits of project investment, and its formula is as follows.

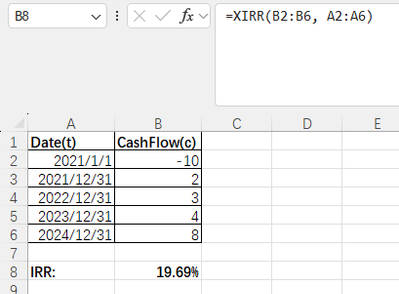
In excel, you can use the XIRR function to calculate the IRR of non-periodic cash flows easily.

But if we want to compute IRRs for thousands of investments and portfolios, we need something like PySpark to do it, which is what I’ve been working on recently.

PyXIRR

In pypi, there is a special library called pyxirr that can help us calculate IRR

# pip install pyxirr

from datetime import date
from pyxirr import xirr

dates = [
    date(2021, 1, 1),
    date(2021, 12, 31),
    date(2022, 12, 31),
    date(2023, 12, 31),
    date(2024, 12, 31),
]
cashflows = [-10, 2, 3, 4, 8]

irr = xirr(dates, cashflows)

print(f"IRR: {irr}")
# IRR: 0.19686311278122343

Based on this, we can write a UDF to use in PySpark, let us demonstrate it next

df = spark.createDataFrame([
   ("p1",   date(2021, 1, 1), -10)
  ,("p1", date(2021, 12, 31), 2)
  ,("p1", date(2022, 12, 31), 3)
  ,("p1", date(2023, 12, 31), 4)
  ,("p1", date(2024, 12, 31), 8)
], ("project", "accounting_date", "cashflow"))

df.createOrReplaceTempView("demo")

def xirr_udf(dates: list, cashflows:list) -> float: 
  return xirr(dates, cashflows)
spark.udf.register("xirr_udf", xirr_udf)

Since the data type received by the UDF is an array, we need group by and collect_list

spark.sql(f"""
with tmp as (
    select
        project
        ,collect_list(accounting_date) as dates
        ,collect_list(cashflow) as cashflows
    from demo
    group by 
        project
)
select
     project
    ,xirr_udf(dates, cashflows)
from tmp           
          """).display()

But due to some limitations of the cluster, I can’t install any package I want, I have to stick with the existing ones, like numpy, scipy, the classics.

The Roots

Looking back at this equation, we can see that the IRR value is the solution that makes it equal to zero. So we can express it like this.

def xnpv(rate):
  """Calculate the NPV for a given rate."""
  return sum(cf / (1 + rate) ** (day / 365.0) for cf, day in zip(cashflows, days))

With the expression of this equation, we can solve its root using Newton’s method. With the help of scipy.optimize

def xirr(cashflows, dates):
    days = np.array([(date - dates[0]).days for date in dates])

    def xnpv(rate):
        """Calculate the NPV for a given rate."""
        return sum(cf / (1 + rate) ** (day / 365.0) for cf, day in zip(cashflows, days))

    try:
        return newton(func=xnpv, x0=0.1)
    except RuntimeError:
        raise ValueError("XIRR calculation did not converge. Try different initial guesses or check inputs.")

Bonus

This function is a simple power function, you can write its derivative, and if you provide a derivative for NetWon, it will calculate the solution faster.

https://en.wikipedia.org/wiki/Power_rule

import numpy as np
from scipy.optimize import newton


def xirr(cashflows, dates):
    days = np.array([(date - dates[0]).days for date in dates])

    def xnpv(rate):
        """Calculate the NPV for a given rate."""
        return sum(cf / (1 + rate) ** (day / 365.0) for cf, day in zip(cashflows, days))

    def xnpv_derivative(rate):
        """Calculate the derivative of NPV with respect to the rate."""
        return sum(-cf * (day / 365.0) / (1 + rate) ** ((day / 365.0) + 1) for cf, day in zip(cashflows, days))

    try:
        return newton(func=xnpv, x0=0.1, fprime=xnpv_derivative)
    except RuntimeError:
        raise ValueError("XIRR calculation did not converge. Try different initial guesses or check inputs.")